Nonlinear photonics and materials

Our theoretical photonics research at Salford is currently focusing on discrete nonlinear Schrödinger (dNLS) equations. These types of governing equations typically prescribe how light waves diffract when they travel through periodic media that have a nonlinear component (for example, where material properties such a refractive index depend upon wave intensity rather than wave amplitude – this optical phenomenon is known as the Kerr effect). The wave in any given channel is linearly coupled to the waves in its nearest-neighbour channels, and nonlinearity provides a mechanism for feedback via a discrete analogue of the self-focusing process. These dNLS systems, like their continuum counterparts, have the potential for exploiting exotic phenomena in the design of future photonic device architectures and information-processing applications.

Much is known about dNLS-based models in a wide variety of experimental contexts, but some fundamental questions remain unaddressed.  We are especially interested in their capacity to generate spontaneous spatial patterns when subjected to a variety of physical boundary conditions encountered in optics, particularly those prescribing ring cavities and counterpropagation.  When starting from perturbed plane-wave inputs, typical patterns that emerge over time tend to include squares (shown below, top row) and hexagons (bottom row).  The squares and hexagons are usually static (that is, unchanging in time), indicative of so-called Turing patterns and that survive in the long term. 

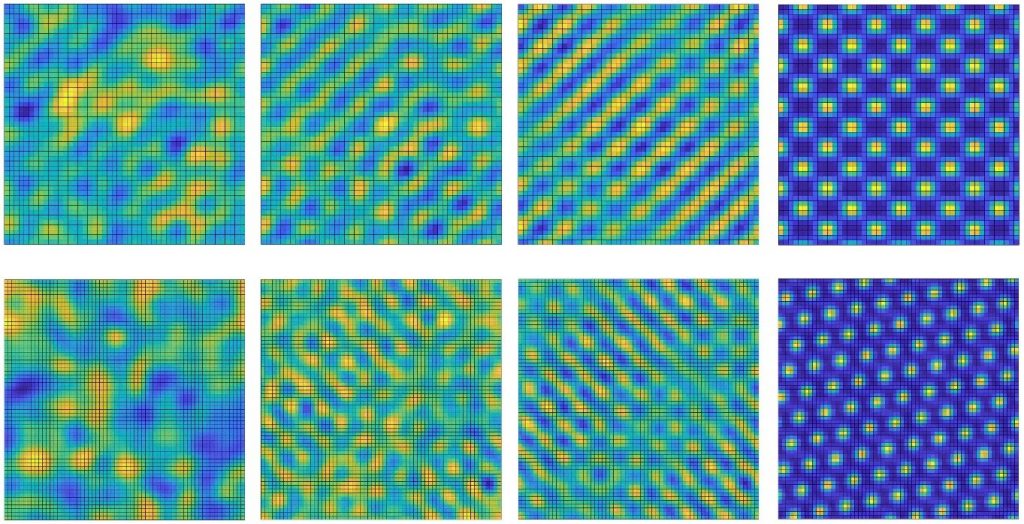
Complementing these dNLS analyses, our attention has recently turned to governing equations of greater interest in the applied mathematics community––the Ablowitz-Ladik (AL) equation––while preserving an emphasis on the role played by boundary conditions.  The AL equation is fundamentally different from its dNLS counterpart, namely that the nonlinearity has a nonlocal character.  Here, the diffraction of the wave in any given channel is now affected by the intensity of the waves in its nearest-neighbour channels.  Through analysis and supporting simulations, we have discovered that some of the most important features of pattern formation (e.g., the emergence of hexagons and squares) remain intact.